Shipping the winning variation
Read time: 2 minutes
Last edited: Jul 29, 2024
Overview
This topic explains how to choose and ship a winning variation for a completed experiment.
Choose the winning variation
LaunchDarkly uses Bayesian statistics in its Experimentation model. The winning variation for an experiment is the variation that is most likely to be the best option out of all of the variations tested. To learn more, read Decision making with Bayesian statistics.
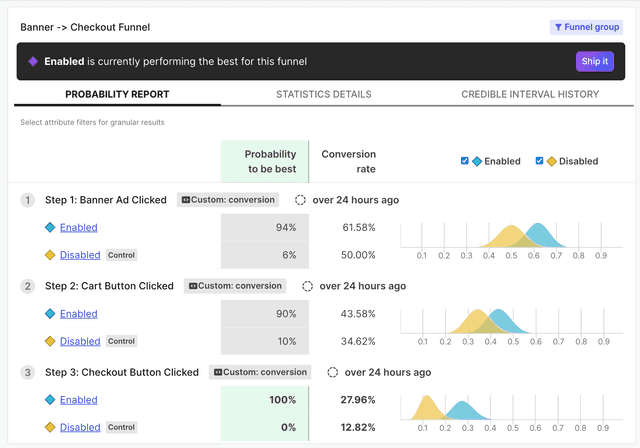
In addition to the variation that had the biggest effect on the final metric in the funnel metric group, funnel optimization experiments also display the winning variation for each step in the funnel. The winning variation is highlighted at the top of the results section.
In this example, the "Enabled" variation has the highest probability to be best:
Ship the winning variation
If enough contexts have encountered your experiment to determine a winning variation, you can stop the experiment and ship the winning variation to all of your contexts.
To ship a winning variation:
- Navigate to the Experiments list.
- Click on the name of the experiment you want to ship a variation for.
- Click on the Results tab.
- Scroll down to the probability chart. If enough contexts have encountered the experiment to determine a winning variation, a winning variation banner is visible.
- Click Ship it. A "Ship the leading variation" dialog appears.
- Click Ship it.
The experiment iteration stops. All contexts are now receiving the winning variation of your experiment. LaunchDarkly retains all of the data collected from stopped iterations.
LaunchDarkly provides additional statistics for further information, but you do not need to use these statistics to make a decision about the winning variation. To learn more, read Statistics details.